Draw the unit square and the unit circle. Consider only the part of the circle inside the square and pick uniformly a large number of points at random over the square. Now, the unit circle has pi/4 the area of the square. So, it should be apparent that of the total number of points that hit within the square, the number of points that hit the circle quadrant is proportional to the area of that part. This gives a way to approximate pi/4 as the ratio between the number of points inside circle and the total number of points and multiplying it by 4 we have pi.
Let's see the python script that implements the method discussed above using the numpy's indexing facilities:
from pylab import plot,show,axis
from numpy import random,sqrt,pi
# scattering n points over the unit square
n = 1000000
p = random.rand(n,2)
# counting the points inside the unit circle
idx = sqrt(p[:,0]**2+p[:,1]**2) < 1
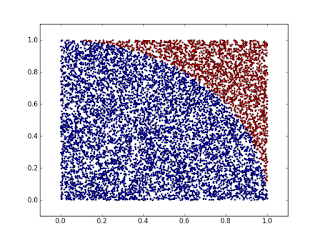
plot(p[idx,0],p[idx,1],'b.') # point inside
plot(p[idx==False,0],p[idx==False,1],'r.') # point outside
axis([-0.1,1.1,-0.1,1.1])
show()
# estimation of pi
print '%0.16f' % (sum(idx).astype('double')/n*4),'result'
print '%0.16f' % pi,'real pi'
The program will print the pi approximation on the standard out:
3.1457199999999998 result 3.1415926535897931 real piand will show a graph with the generated points:
Note that the lines of code used to estimate pi are just 3!

Or you could use the math library in Python and display the value of math.pi
ReplyDeleteIts a tad bit easier.
Hey, you hate experiments! don't you? :)
ReplyDeleteI have not done the calculation of error, but there's a likelyhood that you introduce noise using sqrt in idx = sqrt(p[:,0]**2+p[:,1]**2) < 1. And you don't need to. You can compare the square of the distance against 1 and you're still good.
ReplyDeleteThis comment has been removed by a blog administrator.
ReplyDeleteI really like it : ) I didn't write much code till now and I tried this pi-approximation - now that I saw this nice and short way, I am very jealous : P
ReplyDeletefacinating, I am really impressed.
ReplyDelete